Turing Machine is a competitive board game designed by Fabin Gridel and Yoann Levet. The goal is to uncover a three-digit code using minimal tests. The game features machines with multiple cards, each performing an unknown test. For example, one card might test if one digit is smaller than three, but the specific digit being tested remains a mystery until uncovered through gameplay. Players must strategically use their tests to deduce the correct code.
The game consists of code cards, criteria cards, and verification cards. Code cards represent the code being tested, while criteria cards specify the criteria that each code card could be testing. Verification cards provide the results of whether a code tests true or false for a specific criteria card. Changing the verification card changes the criterion being evaluated.

The Turing Machine is a beautiful and ingenious game. The code cards are perforated, with only one visible perforation when stacked. By aligning the code cards with the verification card, you can see the result of the code for the given criteria. Each square on the verification card corresponds to a possible code, resulting in a total of 125 possibilities. In the provided image, green squares represent codes that are tested as True for that specific machine card.
Finding the right code
Firstly, we prune possible codes based on feasibility for a given machine. It is important to note that not every combination of sub-criteria is valid. Some combinations may have multiple possible codes, while others may have none at all. A valid machine is guaranteed to have only one secret code that tests to True in every criteria.
Secondly, we choose tests that are expected to significantly reduce entropy regardless of outcome. This is similar to the way Akinator works.
Code pruning
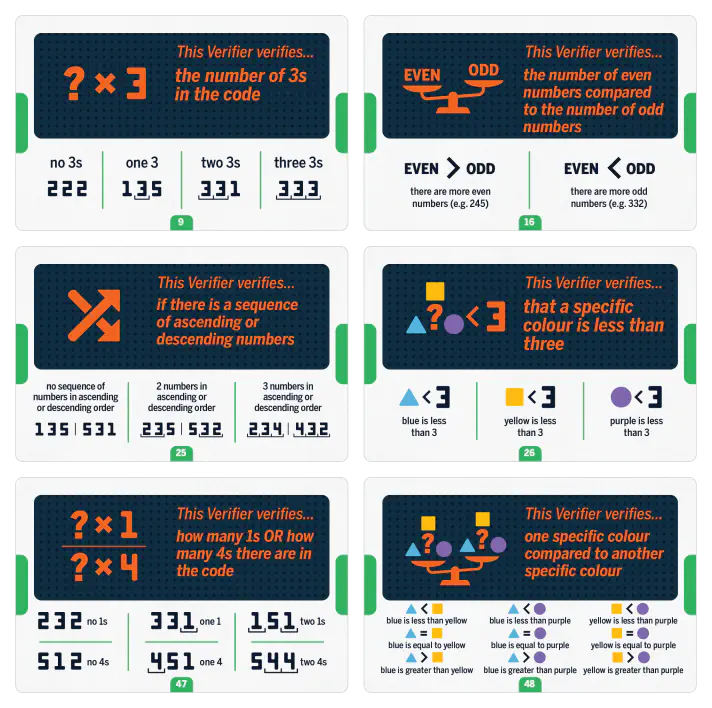
The machine, equipped with criteria cards 9, 16, 25, 26, 47, and 48, can test various potential sub-criteria. Although card 48 alone offers nine possible tests, the machine as a whole can combine these criteria into 3,888 unique configurations.
$$\text{PossibleConfigs} = \prod_{card_i} NumberSubCriteria(card_i)$$Out of these, only 332 form functional machines—those with a single valid code. This refinement process reduces the potential codes from an initial count of 125 to a final selection of just 89 valid options, without using any tests. Subsequently, the appropriate code and corresponding cards are selected for testing.
Choosing the best test
In evaluating the efficiency of code-cracking strategies, we consider the impact of card outcomes on the pool of potential codes. Our method involves systematically testing combinations of up to three cards using the same code. The objective is to choose tests that effectively halve the number of remaining possibilities, regardless of whether the tested cards are true or false. With this approach, on average, it should take approximately \(\log_2(\text{number of codes})\) tests to pinpoint the secret code.
The strategy is designed to follow a ‘safe path’ by ensuring significant reductions in possibilities with each test, optimizing for all possible outcomes. While it is theoretically possible to identify the secret code in fewer tests with an element of luck — for instance, a single true outcome might immediately isolate the correct code — the likelihood is low. Therefore, this algorithm focuses on consistent and predictable progress toward identifying the secret code rather than relying on chance.
Source code
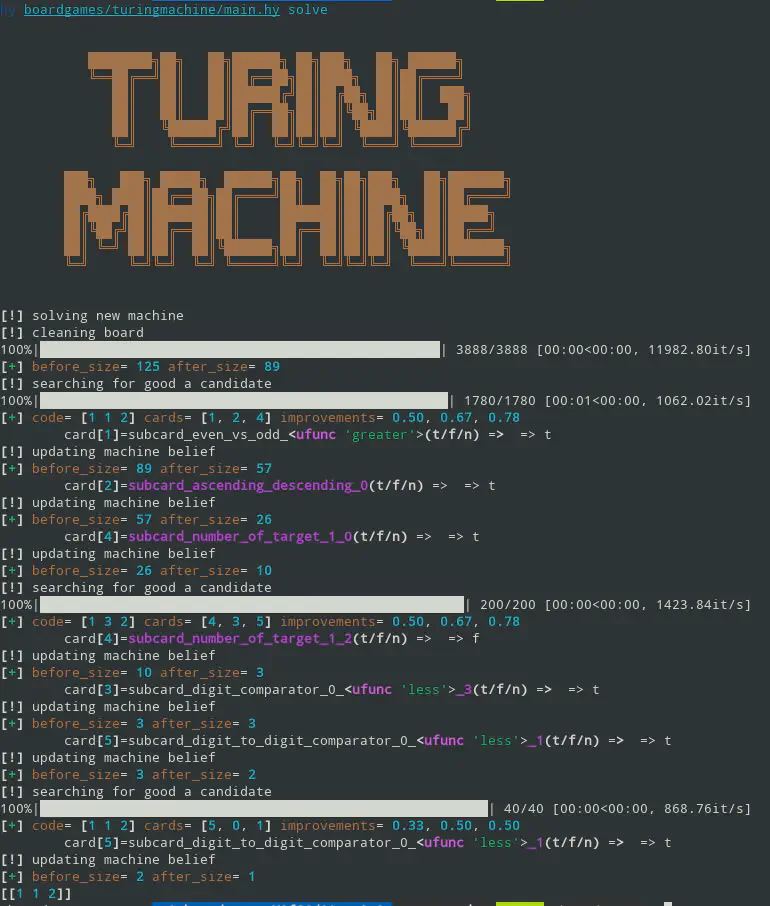
The following image contains one example game. You can find the code for solving Turing Machines in this repository .